I frequently get asked how to calculate standings gain points for the OBP category. In this post I’ll give you an example of how to perform this calculation .
Full disclosure: I don’t play in any OBP leagues.
I know, I know. You just lost a ton of respect for me and you’re considering leaving the site. But I’m here to serve, so let’s figure this out together.
Before we begin, special thanks are in order for reader Matt who graciously agreed to fill out the “What It Takes To Win Your League Calculator” with the last four years of history for the OBP category in his league. You can see the data for ten teams listed below.
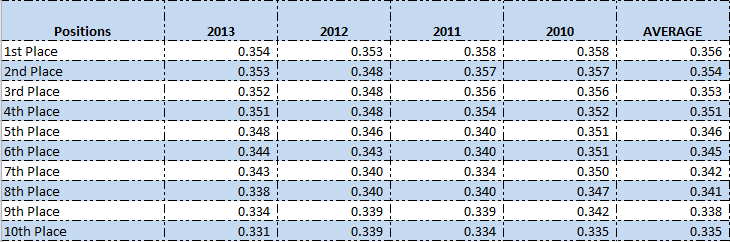
How Many OBP Points Move You Up One Spot In The Standings?
Over the last four years, an average of .356 won the category and an average of .335 finished 10th.
.356 – .335 = .021 total spread between 10 teams
We have the data for 10 teams, meaning there are 9 spots you can move up in the standings by moving from .335 to .356 in team OBP.
.021 / 9 = .00233
On average, increasing your team OBP by .0023 points will result in you climbing one spot in the standings.
But I Play In A 12-Team League, Can I Use This Figure?
If you have an established league history with historic standings available to you, you can always calculate this yourself based upon your league’s specific history.
I don’t have specific evidence to support this, but I would venture a guess that limiting your SGP calculations to the top 10 out of 12 teams might be more beneficial than using all 12 teams. This would minimize or eliminate the effect of teams that lose competitiveness or that tank the season.
What Formula Do I Use To Calculate The SGP For A Given Player?
Recall from Part 5 of the “Create Your Own Rankings” series, that you determine the SGP for a ratio stat, like OBP, by removing the effect an average player has on an average team, and then inserting the player you are ranking into the equation.
- Using the table above, the average OBP for the ten teams was .346.
- If you need a refresher, the formula for OBP is:
(H + BB + HBP) / (AB + BB + HBP +SF)
- This essentially is times on base divided by plate appearances. I’m going to ignore sacrifice flies from the equation because they’ll have a minimal effect on the calculation and they’re not projected by all projection systems.
- Assuming we are trying to calculate SGP for a 12-team league drafting 14 hitters each, that means 168 players will be drafted. The top 168 hitters in my 2014 projections show an average of 580 plate appearances each (I had to calculate this myself by looking at the projections).
- A team with 14 hitters would then have 8,120 combined plate appearances (14 * 580).
- Knowing that the team OBP averages to .346, we can determine that the times on base for an average team is 2,810 (.346 * 8.120). The times on base for the average player is 201 times (.346 * 580).
- The effect of an average player (201 times on base, 580 plate appearances) on the team could be shown as:
=(201 + 2,609)/(580 + 7,540)
- Now remove the average player:
=(X + 2,609)/(Y + 7,540)
- If you’re using the “Create Your Own Rankings” series, the specific formula that would be added to the “Hitter Ranks” tab in your rankings spreadsheet (step 6 of Part 5) would be:
=(([@H]+[@BB]+[@HBP]+2609)/([@AB]+[@BB]+[@HBP]+[@SF]+7540)-.346)/.00233
You might first have to add a column for HBP. I did not have this included in the original instructions for creating your own rankings.
The formula above has a lot going on, but it’s really just trying to find the team’s OBP after removing one average player and inserting the effect of the player you are ranking. The difference between the new team OBP and the historic league average of .346 is determined (this is the reason for the “-.346” part of the equation). The difference is then divided by .00233.
More Info About Matt’s League
The starting lineup in this example league is C, 1B, 2B, SS, 3B, OF, OF, OF, UTIL (9 hitter slots). So this is a shallower league than I use in most instructional posts. If you play in a standard league starting 14 hitters, the OBP numbers in your league will be lower than those shown here. Adding additional players, especially a second catcher and weaker middle infielders, to the lineup will drag down OBP.
If you play in a league where the historical OBP stats are not available, you could use these as a starting point. But I would recommend calculating from your league’s own history if the data is available.
In the end it is the spread from the first team to the last team that drives SGP. It is not the actual OBP numbers themselves. So while the OBP numbers in a 12-team league using larger rosters will be lower than Matt’s standings, the spread between the teams is what’s important. I imagine the spread would be affected by adding more players, but I can’t comment on how significant of an effect it would be.
The Same Concepts Still Apply
Hopefully the illustration above gives you enough usable information and you can follow the calculation process to determine the figures for your own league.
Thanks For Reading
Stay smart.







Would you treat a H2H league as if it was a rotisserie, or is there an adjustment you’d make?
Hi Sean. I think treating a H2H league as if it were a rotisserie league makes sense, but with a couple of caveats. First, it makes sense to have a balanced team early in the season (like in rotisserie), but as the season progresses and the playoffs near, I think it makes more sense to determine a specific strategy for the playoffs that may involve punting a category or two in exchange for strengthening others. Second, there is also an element of “consistency” that becomes important in H2H. I have not done much research into this concept, but others have. Here’s an example: http://www.baseballhq.com/content/head-head-consistency-series-part-i%E2%80%942014-draft-values
First, the denominator I’m using from 1 year of play in my OBP league is .00255. So, pretty close.
Also, how do you treat guys with multiple position eligibility when determining your replacement level player? For example, do you leave Buster Posey in your list of first basemen, even though he obviously has more value as a C?
Seems to me you can only use a guy once, otherwise you will end up with less than the requisite # of players in your final pool.
That’s for a 12-team league, btw.
Hi Dave, thanks for validating the numbers I came up with. I assign multi-position eligible players to the weakest position they qualify for. For example, Posey is treated as a Catcher because of the weakness at that position in comparison to 1B. This gives Posey the most value and is very likely what he will be drafted for.
Thank you very much for this post. Very helpful
How feasible is it to do this for ops?
LYH, I will try to get a post up for OPS in the next couple of days. The data I have is from an NL-only league, so the factors will probably not be indicative of a mixed league, but I can at least display how I would calculate everything.
That would be very helpful. Thanks!
I’m trying to break this down for my 10 team league. =(201 + 2,609)/(580 + 7,540) — maybe i missed it but what is the 2609 and 7540 in the formula?
Hi Jason. I’ll take one step back first. First think of the “=(201+2,609)/(580+7,540)” instead as “2,810/8,120”.
The 2,810 / 8,120 = 0.346 (the league average OBP) for the league shown above.
In this 12-team league with 14 hitters on each team that means 168 players are drafted. I looked at the top 168 players and found that they averaged 580 plate appearances.
The 8,120 = 580 plate appearances * 14 players.
If I have 8,120 plate appearances and know that I had an overall OBP of 0.346, that means there had to be 2,810 “times on base” (8,120 * .346 = 2,810).
So now we’re at 2,810 / 8,120. But that is for 14 “average” players. We need to remove one “average” player and then add back the stats from the player you’re evaluating.
2,810 / 14 = 201 “times on base for the average player”
8,120 / 14 = 580 “plate appearances for the average player”
So removing one of those gets us (2,810 – 201)/(8,120 – 580).
Or 2,609 / 7,540.
Hope that helps.
That was the step i was missing. Thank you for your quick response.