Most of the concepts used in the standings gain points process of valuing players are straightforward. If there’s one facet of the process that causes the most confusion, it’s the handling of ratio statistics like batting average and WHIP. In the piece that follows, I’ll revisit the basics of what makes ratios statistics different and then I’ll get into two very specific and more complicated questions I often see.
- How do you determine the baseline (or league average) ratio to compare the player pool to?
- What if you don’t use an accurate measure for that baseline?
Counting Stats are Simple
A player cannot hit a “negative home run” or “lose strikeouts”. Each counting stat helps you move closer to the next team in the standings. So when we are calculating SGP for a player, the counting stats all evaluate out to a positive number. For example, if we determine based on 2017 standings that it takes 8.526 home runs to move up one spot in the standings, Dee Gordon’s two home runs still calculate out to 0.2346 standings gain points. They’re still beneficial in an absolute sense.
Ratio Stats are Messy
When it comes to rotisserie scoring of ratio stats, we are not judged in that same manner. A player with a poor batting average or a bad earned run average can lower your score within those categories. You can have negative ratios that cause you to lose points or fall in the standings. A player can have a negative SGP for a ratio category.
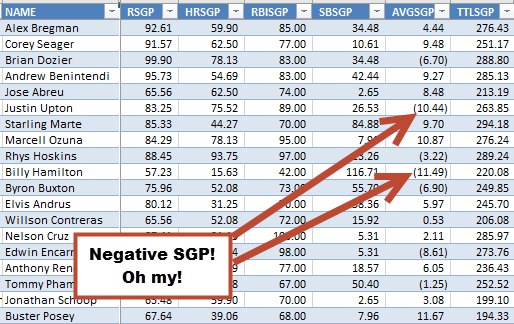
How Do We Calculate SGP for Ratio Stats?
NOTE: This part is a refresher. If you already have a general understanding of how this works, skip down to the next bolded heading.
Let’s revisit how we calculate things for ratio stats. Directly from my guide “Using Standings Gain Points to Rank and Value Fantasy Baseball Players” (with specific text emphasized):
If we assume a league of 12 teams and 14 hitters on each team (adjust for your roster size), that is 168 players (12 * 14). In the Steamer projections, the top 168 major leaguers are projected for an average of about 509 at bats per player.
This means the average team in this fantasy league will have approximately 7,126 at bats (14 players * 509 at bats). According to Razzball, the average rotisserie batting average in 12-team leagues was .267. This means the average team had approximately 1,902 hits (7,126 * .267). And the average player had 136 hits (1,902 team hits / 14 players).
To find the impact of Trout we need to remove one “average” player from the team and then add in Trout’s projections. We can do the same for Tulowitzki.
13 “average” players * 509 at bats = 6,617
13 “average” players * 136 hits = 1,768
Before I start getting into the intricacies of that process, it’s important to understand that the approach we use to calculate SGP for ratio stats is to find an individual player’s effect on that ratio stat for an AVERAGE team in the standings.
Here’s a closer look at how you would do this for batting average:
| Step | Description |
|---|---|
| 1. | You first need to know what your fantasy league’s average batting average was. In this example, let’s say it’s .267. |
| 2. | Determine what the SGP factor is for the ratio stat. In this example, let’s use 0.0019 (the raw factor for the 12-team Online Championships calculated here). |
| 3. | You then need an approximation of how many at bats it took to generate that average. In this example, I determined that 168 players (12 teams * 14 players per team) would average 509 at bats. (more on how this was determined later!) |
| 4. | Using that information, derive the number of hits the average player had. Knowing the league average and the number of at bats, we can easily figure out that the average player would have had 136 hits (.267 * 509 = 135.9). |
| 5. | Next, you extrapolate the 136 hits and 509 at bats per player to team totals. But not a full team of players. ONE LESS PLAYER THAN A FULL TEAM (PER YOUR LEAGUE’S SETTINGS). We’re trying to figure out what an average team looks like without the one player we’re trying to rank.
In this example of a 14-player roster, we’ll use 13 players (one less than a full team). This means the average team (minus one player) would have 1,768 hits (13 * 136) and 6,617 at bats (13 * 509). It’s CRITICAL that these two numbers hold true to your league average stat. Notice that 1,768 divided by 6,617 is still .267. |
| 6. | Then, you add in the projection for the player being evaluated and DETERMINE THE TEAM’S RATIO STAT WITH THAT PLAYER. Assume a player is projected for a .300 average on 200 hits and 667 at bats. The calculation would be:
= (1,768 hits + 200 hits) / (6,617 at bats + 667 at bats) = 1,968 hits / 7,284 at bats = .27018 AVG
|
| 7. | Finally, determine the effect of the individual player by subtracting the average team’s ratio (from step 1 above) from the recalculated team ratio with the player, then divide by the SGP factor.
In our example, this calculation would be:
= (.27018 – .267) / 0.0019 = 1.6737 SGP Instead of using a player with a .300 average, assume we used a player that dragged the team average down to .264. For this player, the SGP calculation would be:
= (.264 – .267) / 0.0019 = -1.5789 SGP Negative standings gain points! I said this cannot happen with counting stats… But it CAN AND WILL HAPPEN with ratio stats. |
How Do You Determine the Baseline (or League Average) Ratio to Compare the Player Pool to?
When you read through that description above, things generally make sense. But when you actually try to reperform that process, you’ll quickly realize I skipped some steps and take some liberties…
I think the biggest issue I leave unaddressed is, “How does one determine the league average number at bats, plate appearances, or innings pitched each team will have?”
Everything in the process revolves around determining the effect one player will have on a league average team. We use last year’s standings to determine what league average BA, ERA, and WHIP were… But that doesn’t address the playing time those ratios stats were earned over.
One big problem is that I’ve never been able to locate public information about the number of at bats or innings pitched a team has. The NFBC standings don’t provide this. A lot of league hosting sites, like Yahoo or ESPN, don’t make this very easy to find either. I don’t have a reliable data set from actual standings to use for this calculation.
Not having this information, I’ve been working around the problem by trying to estimate what the playing time will look like for next season using projections… I’ve never explicitly mentioned this. But do hint at it in this description:
If we assume a league of 12 teams and 14 hitters on each team (adjust for your roster size), that is 168 players (12 * 14). In the Steamer projections, the top 168 major leaguers are projected for an average of about 509 at bats per player.
This seems reasonable, right? But there’s a problem here… It creates a circular calculation.
What that quoted excerpt essentially says is, “Before you can determine the top 168 hitters, you first need to determine the number of at bats of the top 168 hitters.”
You see, in order to determine who the top 168 hitters are, you need to evaluate them on batting average. In order to evaluate them on batting average, you need to know exactly who the top 168 hitters are. But you can’t know one without the other…
Run the Rankings More Than Once
A practical way around this dilemma is to run through the rankings at least twice. Assuming you’re familiar with the basic SGP process, here’s how you can work through this circular calculation issue:
You can repeat the steps above as many times as you wish. You should get to a point where you only see minor shuffling of player rankings and even that should only be at the lower end of the spectrum. Practically speaking, I don’t think there’s much benefit to going through this more than just the two times.
What if You Don’t Use an Accurate Measure for the Baseline?
If I’m being completely honest, there have been seasons where I completely forgot to update these ratio category formulas in my rankings spreadsheets. I just roll last year’s rankings forward, update the player ID map, bring in the new projections, and I’m on my way… Ooops.
This got me to wondering, “How big of a deal was it that I didn’t update those?” Let’s take a look.
Here are the average ratio stats in the NFBC Main Event (15-team leagues) for the last five years:
| Year | AVG | ERA | WHIP |
|---|---|---|---|
| 2013 | .2645 | 3.708 | 1.252 |
| 2014 | .2616 | 3.549 | 1.229 |
| 2015 | .2641 | 3.755 | 1.241 |
| 2016 | .2652 | 3.959 | 1.269 |
| 2017 | .2649 | 4.123 | 1.291 |
How Much Are Rankings Affected?
In order to determine the effect, I’ll compare a rankings set from the lowest batting average year to the highest (2014 to 2016) and rankings from the lowest pitching ratios (2014 to 2017) to the year with the highest.
Here are the other noteworthy assumptions I’ll make when running this comparison:
- Rankings assume a 12-team standard league (two catcher, five OF,
etc.) (Sorry, as I proofread this I realize that I just switched from a 15-team discussion to a 12-team one) - Steamer 2018 projected stats (as of January 21, 2018) are used for the comparison
- SGP factors are from the 2017 12-team NFBC Online Championship
- Budgets are allocated 67% to hitting, 33% to pitching
You can see the comprehensive listing of all players and how there were affected here. You can see all hitters here. And all pitchers here.
Effect on Hitters
Here are the most significant changes in hitters:
| Player | AVG | High Ratio $ | Low Ratio $ | Change $ | High Ratio Rank | Low Ratio Rank | Change Rank |
|---|---|---|---|---|---|---|---|
| Mike Trout | .310 | $42.97 | $42.70 | $0.27 | 1 | 1 | 0 |
| Giancarlo Stanton | .284 | $38.27 | $38.02 | $0.25 | 2 | 2 | 0 |
| Bryce Harper | .303 | $30.83 | $30.58 | $0.25 | 7 | 8 | 1 |
| Elvis Andrus | .280 | $15.45 | $15.84 | -$0.39 | 55 | 49 | -6 |
| Jose Peraza | .277 | $8.60 | $8.98 | -$0.38 | 95 | 93 | -2 |
| Asdrubal Cabrera | .261 | $0.93 | $1.28 | -$0.35 | 169 | 164 | -5 |
Realistically, nothing changed for the hitters. A handful of guys moved slightly, but the changes were minimal. Remember, we’re talking about a change in the baseline batting average of .261 to .265. Out of a season of 510 at bats, this is only two hits!
If it looks odd that the top tier players gained, it is more a function of them being outfielders. The change in valuing of ratio stats did change those players specified as replacement level and this change served to give outfielders a slight bump and dinged the shortstops a bit.
Effect on Pitchers
Pitching is a bit of a different story. Here are the notable changes for the pitchers:
| Player | High Ratio $ | Low Ratio $ | Change $ | High Ratio Rank | Low Ratio Rank | Change Rank |
|---|---|---|---|---|---|---|
| Clayton Kershaw | $36.24 | $34.16 | $2.08 | 1 | 1 | 0 |
| Max Scherzer | $30.79 | 28.87 | $1.92 | 3 | 3 | 0 |
| Kenley Jansen | $20.71 | $22.22 | -$1.51 | 11 | 6 | -5 |
| Craig Kimbrel | $18.50 | $20.05 | -$1.55 | 15 | 11 | -4 |
| Madison Bumgarner | $19.41 | $17.69 | $1.72 | 14 | 15 | 1 |
| Jose Quintana | $21.12 | $19.60 | $1.52 | 10 | 12 | 2 |
| Andrew Miller | $7.22 | $8.95 | -$1.73 | 56 | 44 | -12 |
| Marco Estrada | $1.00 | $0.14 | $0.86 | 108 | 116 | 8 |
As a reminder, the low ratios refer back to 2014 when fantasy league average ERA was 3.549 and WHIP was 1.229. The high ratios refer to 2017, which had an ERA of 4.123 and a WHIP of 1.291. We are talking about a 0.60 change in ERA and a 0.06 change in WHIP. Nothing to sneeze at.
What you see above is that relievers fared much better in the “Low Ratio” setup. When the”High Ratio” setup is applied, the relievers fell in the rankings.
This Doesn’t Make Sense
Hold the phone. My initial reaction when seeing this was, “You’re trying to tell me, that if I move Andrew Miller from a low run scoring environment to a high scoring environment, HE LOSES VALUE? A guy with an ERA below 2.00? Get outta here.”
But let’s take a step back and think about what’s really happening here. We’re not JUST moving Andrew Miller to the new environment. All pitchers are being evaluated against the new league average measures. So one cannot just consider how Andrew Miller’s ratios compare to the new league standards. You have to compare him relative to all other pitchers.
When you consider why Miller might actually be harmed in this scenario, there are two reasons:
- Think back to earlier when we established that you can earn negative SGP in ratio categories. When you previously compared all pitchers to an ERA of 3.549 and you now compare them to a standard of 4.123, many more pitchers now move into a positive SGP for earned run average. Miller was already there. He’s earning more SGP for ERA than he did previously, but now a lot of starters are earning more too.
- The magnitude of the change in the first bullet is also affected by the number of innings a pitcher throws. Miller is a reliever. He might only throw 65 innings. Whereas a starter might be projected for 150 or more. A pitcher that throws 150 innings can move your team’s ERA more than a reliever that throws 60, even if he has a higher ERA than the reliever.
Here are some actual numbers to help visualize this. Assume we’re comparing two hypothetical players.
| PLAYER | IP | ER | ERA |
|---|---|---|---|
| Starter | 150 | 50 | 3.00 |
| Reliver | 65 | 21.67 | 3.00 |
Yeah. A pitcher can’t give up 21.67 earned runs. But go with me here. We have two pitchers, both with an ERA of 3.00. What happens to a team’s ERA if one of them is added? Let’s look under the high and low ratio environments. For the sake of this illustration, we’ll assume the league average pitchers have 110 IP.
| Player | IP Before | ER Before | ERA Before | IP W/ | ER W/ | ERA After | Effect |
|---|---|---|---|---|---|---|---|
| Starter | 1,430 | 563.9 | 3.549 | 1,580 | 613.90 | 3.497 | -0.052 | Reliever | 1,430 | 563.9 | 3.549 | 1,495 | 585.57 | 3.525 | -0.024 | Starter | 1,430 | 655.10 | 4.123 | 1,580 | 705.10 | 4.016 | -0.107 | Reliever | 1,430 | 655.10 | 4.123 | 1,495 | 676.76 | 4.074 | -0.049 |
There’s a lot going on here. But focus on the rightmost column. Regardless of the “league average” environment used, a starter can move a team’s ERA more than twice as much as a reliever with the same ratios (they pitch more than twice the number of innings. Thus, when we increase that “league average” environment, a starter benefits more from that than a reliever does.
So why didn’t that happen? The reason is that the inputs into this test are 2018 projections. The run scoring environment is so much different now, it’s pretty rare for a starter in 2018 to be projected for an ERA below the 3.549 average. It’s more common for a reliever to be projected below that level. This means that all of those starters with ERAs above 3.549 were being artificially devalued. Instead of earning positive SGP, they were being assigned negative SGP. As soon as you start comparing those 2018 projections to the higher ratios, many more starters start showing positive SGP. They start gaining on the relievers. And because of the magnitude effect of their innings pitched, they start becoming more valuable than some relievers.
Why Do You Use Last Year’s Standings Ratios?
I mentioned above that when doing my rankings, I compare players ratio stats against the league average standings ratios from last season. Said another way, I’m using fantasy standings data from LAST YEAR to determine how a player ranks THIS YEAR.
This is just one of three possible ways I can see for evaluating players. All three are:
- Evaluate against fantasy league average standings ratios from last season
- Evaluate against the ratios of last season’s ACTUAL top valued hitters and pitchers
- Evaluate against next season’s PROJECTED top valued hitters and pitchers
I use the first option. But I figured I’d investigate option #2. I quickly identified an issue here… When I run a ranking of the top 108 pitchers based on actual production from the 2017 season, the total ERA of that group comes out to 3.460. The average ERA for a 12-team league was over 4.00! This shows how ineffective we fantasy managers are at identifying the best players in the season.
The reason it’s so low is because many relievers with good ratios end up outproducing starting pitchers that have bad ratios. It’s similar to the effect I just discussed with relievers losing value to starters in a different run scoring environment. Despite this, we’ll continue to trot a guy with a 4.50 ERA and 1.50 WHIP out there.
It seemed wrong for me to compare this year’s player projections against this harsh reality. While I do expect we’ll see some shift in mindset toward the fantasy community being more open to rostering strong non-closing relievers, I know many are still going to be drafting the Matt Moore types.
What I might consider though, is switching to the third option. That of comparing players against those projected to be the best in the upcoming season. I see the logic behind doing this. Afterall, this entire process is dependent upon the projections being used. If I trust them so much, why not use them for one more piece of the ranking puzzle?
My reluctance to switch stems from the same reasons I didn’t like using last year’s actual top players. The ratio stats from that process will not mirror what I think the end standings will look like. I don’t think the fantasy community is going to fully buy into the shift toward deploying effective middle relievers… Yet.
The experiment above showed that the higher run standings environment gives a slight edge to starting pitchers and devalues relievers some. If I don’t think others are going to shift, I want to make sure I’m using a set of rankings that are consistent with that belief.
If that’s the landscape I’ll be playing in, I should rank players accordingly.
Conclusions
Hopefully you’ll walk away from here with a deeper understanding of the finer intricacies as to how ratio statistics can affect the SGP ranking process. This was even a benefit for me to write. My key takeaways are:
- I have a more defined understanding of how and why I use next year’s projections to determine the playing time components of ratio stats.
- I understand the effect a change in environment can have on rankings (and the importance of updating that in my SGP calcs).
- If I see the fantasy landscape becoming more efficient at deploying pitchers, I might need to shift the way I perform these calculations.
Have Any Questions?
Wow. This was a workout. I’m sure for you and me both! If you have any questions, please ask in the comments or follow me on Twitter and ask there.
Good luck this season. Stay smart.







Tanner, first off good analysis. Appreciate the additional context this provides to your SGP method. As a 4th option (or option 1b) to determining a baseline (league avg) for the ratio categories, any reason you don’t suggest a 2-3 year “fantasy league average standings ratio” or 2-3 year weighted avg. (with slight leaning toward most recent year)? I tend to believe most projection sites/systems look at a 2-3 year history of player stats as a starting point for making current year projections (then make some adjustments for player age/trend/changes to mlb enviroment/gut feeling/etc). So to me it would seem to make sense to use an average(or weighted avg) of most recent 2-3 fantasy seasons league average ratio stats (assuming your league settings/#of teams stay the same from year to year) to potentially better align with projections being used for current season. I assume using an average of multiple year league average ratio stats would also mean you would need to use the avg. SGP factor for the same time period in the SGP calculation. Interested if you have ever explored this theory and found a flaw that makes you not consider it, or if you haven’t previously explored, if you see any potential flaws in this theory/method? Appreciate your thoughts.
Hi Adam,
Sorry for the delayed response here. I somehow missed seeing your comment.
You are correct in that I think most projection systems use some kind of 2-3 year weighted average, giving the most weight to the most recent season. I do think this is probably the wisest way to handle these ratio stats.
I have never studied if there seems to be a benefit to doing some kind of weighted average on your own league’s SGP factors. If I was using just my own league’s standings history, I would definitely use some kind of average of past seasons. I think using just one year from one league could misrepresent things.
Now that I’ve figured out how to get the standings data from the NFBC, I think using a single year is acceptable, because those factors are calculated from many leagues. But you may be right, it might even be better to do a weighted average of that data and incorporate some data from prior years.
Hope that helps.
Tanner