Welcome to the fifth part of the “Create Your Own Fantasy Baseball Rankings” series. If you missed an earlier part, you can find it here. You can start at the beginning of the series or if you want to start here at Part 5, you can download the Excel file created during part 4 here.
Please note that this six part series has been adapted into a 10 part book that also shows you how to convert standings gain points into dollar values and how to calculate in-draft inflation.
A few notes about the series:
- It was originally written before the 2013 MLB season. The screenshots and player references you see might refer to things from that time frame, but the same approach will work today.
- If you register as SFBB Insider, you can receive all six parts in a free, tidy, and easy-to-use e-book
- Familiarity with Excel is recommended, but I do my best to explain all formulas and functions used
- Some of the formulas used in the series do not work in Excel for Mac computers. I apologize for this. I don’t understand why Excel isn’t built to operate the same on that platform.
In this fifth part of the series we will discuss the concept of Standings Gain Points (SGP), a method of evaluating and ranking players. At the end of this part, we’ll actually have some primitive rankings in place. But we have quite a few concepts to go over before we jump into Excel.
THE DIFFICULTY IN RANKING PLAYERS
Which player is worth more and should be ranked higher?
- Player A – .280, 65R, 30HR, 95RBI, 0SB
- Player B – .265, 100R, 10HR, 55RBI, 40SB
Or how about this?
- Player A – .280, 65R, 30HR, 95RBI, 0SB
- Player C – 5W, 40SV, 75SO, 2.50ERA, 1.10 WHIP
How do you rank different types of players (speed/average vs. power/RBI)? Or even worse, how do you evaluate the worth of a hitter against the worth of a pitcher? Enter the concept of Standings Gain Points.
STANDINGS GAIN POINTS – MY INTERPRETATION
The end goal of rotisserie fantasy baseball is to accumulate the most points in the standings. The Standings Gain Points approach to valuing players is to convert a player’s statistics into the number of rotisserie points those statistics are worth.
Let’s use some example statistics from a real 12-team 5×5 rotisserie league to illustrate:
| POS | HR | RBI | W | ERA |
|---|---|---|---|---|
| 1 | 291 | 1,054 | 108 | 3.359 |
| 2 | 287 | 1,027 | 107 | 3.365 |
| 3 | 281 | 1,017 | 93 | 3.477 |
| 4 | 274 | 1,003 | 92 | 3.678 |
| 5 | 272 | 998 | 88 | 3.815 |
| 6 | 267 | 973 | 88 | 3.857 |
| 7 | 263 | 968 | 84 | 3.946 |
| 8 | 261 | 965 | 82 | 4.096 |
| 9 | 244 | 945 | 82 | 4.097 |
| 10 | 239 | 921 | 81 | 4.177 |
| 11 | 234 | 920 | 81 | 4.284 |
| 12 | 191 | 792 | 78 | 4.361 |
The first place finisher in Home Runs accumulated 291 HR for the year. The last place finisher accumulated 191. That leaves a spread of 100 HR from the first place team to the last place team (291 – 191 = 100).
In this 12-team league, there are 11 standings points that can be gained (even the last place team gets 1 point, the first place team 12, so 11 points can be gained).
This means that it takes roughly 9.1 home runs to move up one position in the home run standings (100 HR gap / 11 positions to move). Pick just about any position in the home run list, add 9 HR, and you can see that you do move up about 1 spot.
Running the numbers for the other statistics, we get:
RBI: (1,054 – 792) / 11 = 23.82
W: (108 – 78) / 11 = 2.73
ERA: (3.359 – 4.361) / 11 = -0.091
A Better Method of Calculating
The weakness in the calculation method outlined above is that it really only considers the first place team and the last place team. The ideal calculation would consider all teams’ final stat totals. Fortunately, Microsoft Excel offers the SLOPE function that allows us to consider each team, not just the first and last place finishers. You can read more about how to use this formula in a three part series here (Part I, Part II, Part III).
Do I have to calculate these myself?
You could. It would probably be best to calculate using your league’s specific history. Or Razzball has calculations from their average 12-team fantasy league you can review here (or if you really want to rub geek juice all over your body, check this out). For what it’s worth, I’ve been calculating this for my long-time standard mixed 12-team roto league ($260 auction budget, 14 hitters, 9 pitchers) and the results come amazingly close to Razzball’s findings:
| Category | Razzball (based on 48 12-team leagues in 2012) | My League (based 9 year history, 12-teams) |
|---|---|---|
| R | 24.6 | 22.02 |
| HR | 10.4 | 8.87 |
| RBI | 24.6 | 22.31 |
| SB | 9.4 | 8.19 |
| AVG | .0024 | .0017 |
| W | 3.03 | 2.96 |
| SV | 9.95 | 5.70 |
| SO | 39.3 | 31.62 |
| ERA | -.076 | -.088 |
| WHIP | -.015 | -.0152 |
CALCULATING SGP FOR A PLAYER – COUNTING STATS
Steamer’s Projections predict 26 HR for Mike Trout. If I conclude to use Razzball’s calculation that every 10.4 HR is equal to a one position increase in the rotisserie standings, then Mike Trout’s HR equal a 2.5 point increase in the standings (26/10.4 = 2.5). Or 2.5 Standings Gain Points.
Other statistics similar to HR, where players simply accumulate or “count” the statistics one-by-one are referred to as “counting stats”. These are easy to calculate SGP for. Simply take the number of the counting stat (Trout’s 42 projected SB) and divide by the quantity of the stat required to move up one standings point (per Razzball, 9.4 SB to move up one position). So Trout’s 42 SB are worth 4.46 SGPs (42 / 9.4).
For pitchers, wins, saves, and strike outs are also “counting stats” and allow for easy calculation of SGP.
But what about batting average, ERA, and WHIP?
CALCULATING SGP FOR A PLAYER – RATIO STATS
AVG, ERA, and WHIP are referred to as “ratio stats”. The calculation of SGP for these is a bit more involved. Think about this scenario…
Mike Trout is projected for 619 at bats. He’s projected to hit .297 (184H/619AB).
Troy Tulowitzki is projected for 434 at bats. He’s projected to hit .300 (130H/434AB).
Which player will have a bigger impact on your team’s batting average? Does the fact that Trout will hit .297 over nearly 200 more at bats make him more valuable? Or does Tulowitzki’s .300 average make him the better “batting average contributor”?
Let’s run the numbers. If we assume a league of 12 teams and 14 hitters on each team (adjust for your roster size), that is 168 players (12 * 14). In the Steamer projections, the top 168 major leaguers are projected for an average of about 509 at bats per player.
This means the average team in this fantasy league will have approximately 7,126 at bats (14 players * 509 at bats). According to Razzball, the average rotisserie batting average in 12-team leagues was .267. This means the average team had approximately 1,902 hits (7,126 * .267). And the average player had 136 hits (1,902 team hits / 14 players).
To find the impact of Trout we need to remove one “average” player from the team and then add in Trout’s projections. We can do the same for Tulowitzki.
13 “average” players * 509 at bats = 6,617
13 “average” players * 136 hits = 1,768
Add Trout’s projections (184 Trout hits + 1,768 other hits) / (619 Trout ABs + 6,617 other ABs) = .26976
Add Tulowitzki’s projections: (130 Tulowitzki hits + 1,768 other hits) / (434 Tulowitzki ABs + 6,617 other ABs) = .26918
So despite his lower batting average, Trout’s impact on the team batting average is greater than Tulowitzki’s, due to the number of at bats. It’s this weighting we have to take into account for “ratio stats”.
To finish the example, if the team batting average with Trout is .26976 and the team batting average without Trout is .267, he increases the team average .00276 (.26976 – .267). Looking above again, Razzball calculates that a .0024 increase in BA equals one point in the rotisserie standings. This makes Trout’s BA worth 1.15 SGP (.00276 / .0024).
Enough concepts. Let’s rank some flippin’ players.
STEP-BY-STEP INSTRUCTIONS
These instructions will help convert the statistics in our rankings spreadsheet into Standard Gain Points so we can begin to rank players.
- Open your existing rankings spreadsheet (if you don’t have one started, you can download from part 4 here).
- Add five new columns to the “Hitter Ranks” sheet. Do this by typing in column headers beginning in the first empty column to the right of your existing data. Name the new columns RSGP, HRSGP, RBISGP, SBSGP, AVGSGP (as in “Runs Standings Gain Points”, “Home Runs Standings Gain Points”, etc.).
Because we have this sheet formatted as an Excel table, as soon as the column header is added, the entire column will be added to the table. - After you’ve added these five columns, add a sixth column named “TTLSGP”. This will calculate the total SGP across the five hitting categories.
- Add five new columns to the “Pitcher Ranks” sheet. Do this by typing in column headers beginning in the first empty column to the right of your existing data. Name the new columns WSGP, SVSGP, SOSGP, ERASGP, WHIPSGP (as in “Wins Standings Gain Points”, “Saves Standings Gain Points”, etc.).
- After you’ve added these five columns, add a sixth column named “TTLSGP”. This will calculate the total SGP across the five pitching categories.
- Let’s assume a 12-team league and that Razzball’s estimate of the statistics needed to move up one spot are accurate. The formulas to add to the Hitter Ranks columns added above in step 2 are:
Column Excel Formula RSGP =[@R]/24.6 HRSGP =[@HR]/10.4 RBISGP =[@RBI]/24.6 SBSGP =[@SB]/9.4 AVGSGP =(([@H]+1768)/([@AB]+6617)-0.267)/0.0024 TTLSGP =[@RSGP]+[@HRSGP]+[@RBISGP]+[@SBSGP]+[@AVGSGP] - The formulas to add to the Pitcher Ranks columns added above in step 3 are:
Column Excel Formula WSGP =[@W]/3.03 SVSGP =[@SV]/9.95 SOSGP =[@SO]/39.3 ERASGP =((475+[@ER])*9/(1192 + [@IP])-3.59)/-0.076 WHIPSGP* =((1466+[@H]+[@BB])/(1192+[@IP])-1.23)/-0.015 TTLSGP* =[@WSGP]+[@SVSGP]+[@SOSGP]+[@ERASGP]+[@WHIPSGP] - You can now sort both the Hitter Ranks and Pitcher Ranks by the new TTLSGP column to see the “best” players. To sort, click the downward pointing arrow on the TTLSGP column. Then select “Sort Largest to Smallest”. Hit OK to perform the sort.
- As the calculations stand right now (there are some additional changes to be made in Part 6 of the series), the top ten hitters are:
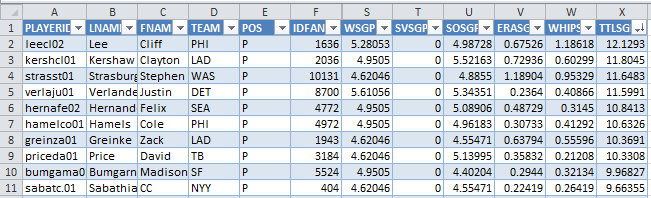
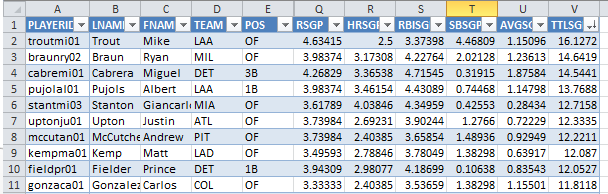And the top ten pitchers are:
WRAP UP
The rankings look pretty good, eh? They’re mostly consistent with the consensus rankings you can find anywhere on the web. But they can also unearth some hidden gems. Cliff Lee as the projected #1 pitcher? Pretty interesting when he’s being drafted #35 in ESPN drafts (at the time this article is being written).
In the next part of the series we investigate the theories of “replacement level players” and “position scarcity”. We will adjust our calculations for these theories in an effort to better fine tune the rankings.
I’ve included some more in depth discussion below. It’s not necessary to read, but I feel the need to acknowledge some weaknesses in the SGP approach.
LINK TO DOWNLOAD FILE: SFBB Rankings – Part 5.xlsx
DISCLAIMER
I prefaced this SGP discussion by saying this is “my interpretation”. I do this because I’m not a mathematician. And I’m certain that there are mathematical errors or logic flaws in my presentation. But in general, I believe the approach is sound. I am aware that there is widespread dispute in the theory behind standings gain points (some think it makes no mathematical sense). Here are my thoughts on the dispute:
- When I look at what these SGP calculations kick out, they pass the eye test. They look right. They make sense.
- In the article link above, Todd Zola points out that the main flaw in SGP versus more mathematically sound approaches is that stolen bases are undervalued by SGP. Sluggers that steal very little are overvalued by SGP.
- I DO NOT SUGGEST you use SGP as a means of constructing a team. I only use SGP as a vehicle to rank players. Said another way, I don’t build a team thinking I need to draft players that will add up to 12 SGPs in a category. I only use the rankings as a barometer of when I should draft certain players.
- Drafting solely based upon Total SGPs is not wise, as it can lead to an unbalanced team. I prefer to draft with “What it takes to win your league?” in mind. I know that it takes about 200 SB to win the category. So I draft players to reach 200 SB. Not 12 SB SGPs.
- I don’t believe in a purely quantitative and statistical approach to drafting players either. There are a lot of qualitative factors that projections, rankings, SGP, or any other valuation method cannot account for. Age, potential, likelihood of injury, competition for playing time, contract situation, and other factors that need to be taken into account. I create rankings and then adjust those rankings for these multitude of other factors.
With all this in mind. I’m fine with SGP being an imperfect system.Part of being “smart” is knowing when good enough is good enough.
* Note About Pitching Rate Calculations
My approach to calculating SGPs for pitching rate categories is based on the following assumptions:
- 12-team league * 9 pitching spots = 108 pitchers rostered
- To calculate a baseline for the rate statistics, I perform a rough exercise to approximate the 108 pitchers most likely to be rostered. I include the 108 pitchers with the highest strikeout numbers and with a projected ERA below 4.20.
- The top 108 strike out pitchers with an ERA below 4.20 in the Steamer projections have an average of 149 IP.
- This means an 8 pitcher staff has a total of 1,192 IP
- According to Razzball, the average rotisserie team in a 12-team league had an ERA of 3.59 and WHIP of 1.23
- To have an ERA of 3.59 on 1,192 IP assumes 475 ER allowed
- To have a WHIP of 1.23 on 1,192 IP assumes 1,466 BB and H allowed (BB+H)
- This makes the ERA formula = ((475 ER + pitcher’s projected ER)*9/(1,192 IP + pitcher’s projected IP)-3.59)/-0.076
- This makes the WHIP formula = ((1,466 H and BB + pitcher’s projected BB + pitcher’s projected H)/(1,192 IP + pitcher’s projected IP)-1.23)/-0.015
IF YOU’VE MADE IT THIS FAR…
You might be interested to know that I’ve recently completed parts 7 through 10 of the “Create Your Own Rankings” series. These additional segments include the calculation of dollar values and incorporate calculations for keeper and in-draft inflation. All ten parts of the book are now available in Kindle format at Amazon. Please click here to read about these additions to the guide and how you can purchase all 10 parts. My hope is that this series is the best step-by-step guide to calculating SGP-based dollar values and inflation is available anywhere.
Please post your questions or suggestions to improve the rankings system in the comments here.
How would you calculate era and whip? And say a specific ratio like k/bb? Thanks for the great work.
The calculations for ERA and WHIP are documented at the very end of the article under the section “* Note About Pitching Rate Calculations”.
K/BB is interesting. Remember there are two things you will need to calculate:
1. The increase in K/BB required to move up one spot in the standings. To calculate that, take the average ratio of the category winner for the last several years and subtract the average ratio of the last place team in the K/BB ratio category for the same period. Then divide that difference by 11 (assuming a 12 team league).
2. You need to weight each player’s K/BB performance and figure out their effect on an average team. I’m wildly speculating because I don’t have data to draw from, but assume the average team in your league had 1,300 Ks and 400 BBs, or a ratio of 3.25 K/BB.
For a 9 pitcher staff that’s 144 K per pitcher and 44 BB. So an 8 pitcher staff would have had 1,152 K (144 * 8) and 352 BB (44 * 8). If the pitcher you are evaluating has 200 K and 60 BB, he would bump the ratio from 3.25 up to 3.28 (1,152 + 200)/(352 + 60).
Then divide this increase by the answer from the first bullet in this comment. (.03 / XX)
This may seem like a rather simple question, but how do you add the formulas so that they automatically calculate the SGP for say wins, saves, etc.? I added the formula in the column, but it didn’t do anything, the column is blank still. Please help.
Tanner,
Also, looking at the Excel chart posted with this page. I cannot find the SGQ ERA based on your ERA formula. Give me an example please of how you end up with a specific SGP for a P.
John, I’m going to e-mail you in order to try to address your questions. I think it will be more effective than using the comments because I need some additional information from you. Thanks.
I have been Commissioner and founder of the Rockland County NY, Roto League since 1981 and have to congratulate you on the most clear and precise explanations of the SGP method. Well done. The average seniority in our league is 24 years and no one has come close to explaining SGP. in fact, I am going to translate our historical stats based upon your method. By the way , we are a 6×6 non keeper ultra league rostering 12 hitters, 9 pitchers and 2 reserve spots for $250. Have you compared SGP with PVM? If so, what’s the variation, if any?
Against, thanks and I look forward to future articles.
Regards,
Don Mallo
Don, thanks for the high praise! I have not done a direct comparison to PVM. But I do want to do that this year before the season starts, so please stay tuned to the site.
How’d you calculate .0024 above for AVG?
Hi John,
I personally track the exact history of my own leagues, but that’s just one league and the people in my league might be fundamentally different than the “average” league. So instead, for this post I just use the numbers that Razzball calculates from their reader leagues. I think they had 48 different leagues they combined and averaged out to get the numbers above (the .0024 BA).
Here’s the link to the Razzball page
For example, one of my leagues last year (you probably want more than one year’s history) the first place team had a .2718 BA. 12th place was .2598. Figure out the total spread in the category (.2718 – .2598 = .012) and divide by the number of teams minus 1 (12 -1 = 11).
.012 / 11 = .0011
That .2718 to win batting average is low. A lot of us were tightly bunched. If you had a .280 to win, the .0011 might come closer to .0024.
Batting average in the league is changing. So that .0024 could be in flux. Hopefully Razzball puts out a similar piece this year.
Thanks, Tanner
Looking forward to your article on PVM. Will be interesting to compare the rankings. Getting back to SGP for a moment. Have you posted an article on translating the SGP scores into dollar values? I have created a sheet using our 16 team 12 category league but am unsure if my method is correct. Our total pool is $4000 (250 x 16) and I have allocated this pool between hitting and pitchers on a .70/.30 ration for simple math. This leaves $2800 for hitters and $1200 for pitchers.
I then calculated the total number of points achievable by league members for the 6 hitting and 6 pitching categories in our 16 team league (1644 total points with 822 for hitters and 822 for pitchers) and divided these results into the appropriate dollar allocation to obtain a dollar value per point. (Our league uses an extra point for 1st place in a category so that the leader gets 17 points and the 2nd place team gets 15).
I then multiplied the dollar value per point by the appropriate SGP number using your methodology to obtain a dollar value.
Would appreciate your insight.
Thanks again for a great and well-presented series.
Don, you have hit on one of the “mathematical flaws” in the SGP approach. Your concept of calculating that there are 1,644 points available is sound (although I’m not sure you would include that bonus point in your calculation). And then calculating a $/point also makes theoretical sense.
But a funny thing happens when you use SGP. If you go and add up all the SGPs for the top 224 hitters and 144 pitchers (assuming 16 teams, 14 hitters, 9 pitchers), you won’t come up with 1,644 points. That’s what drives mathematicians nuts about SGP.
So for calculating your dollar values, you would instead calculate the total SGPs projected for your top 224 hitters. Use that to figure out the dollar value per hitting SGP. Then multiply each hitter’s own SGP by that amount. Then do the same thing for hitters.
I think you need to keep hitters and pitchers separated when you are calculating your $/SGP, because of this phenomenon where the actual projected SGPs are not going to equal the 822 points for hitting and 822 points for pitching.
You also will need to build in a few error checks into your calculations. You need to make sure that your last player is worth $1 and that your top 224 hitters includes 32 C, 48 CI, 48 MI, 80 OF, and 16 other players to fill the UTIL spot. No player in that top 224 should have a negative value.
How do you handle outlier historical data? I’m in a 10 team NL only 4×4 (OBP instead of Avg) and its hard to find reliable values for that setup so this year I’m giving SGPs a shot this time around. Our league has historical data going back to 2001 (the league has actually been around since 1988) so getting the data for the counting stats is very easy. Unfortunately for the rate stats our website has only recorded the final number and not the components (PAs, IP, Hits, etc) that went into those final numbers. As this is not a common league finding a compilation of data like Razzball has on a 12 team 5×5 mixed is a little hard to do.
I think I have found a decent way around this. On the site I can get the player stats for each season and so I pulled that data and came up with a yearly average OBP from the Top 140 players that the site lists (exactly how their rankings are calculated I’m not sure). I’m looking at data from 2009-2013 and for three of those seasons my average OBP is a perfect median number and one of the years its only off by one (four above, 6 below).
However 2009 is super funky. When I calculate the average OBP my result would have place between 7th and 8th which isn’t that close. The interesting thing is that this average is the highest average of the five year period I am looking at, the recorded OBPs for that season were apparently insane. Looking at the data I noticed that season’s AB’s and Hits were about 10% less than the 2010-2013 data (which were all remarkably consistent). I’m having a hard time reconciling how my “average” OBP (once again I’m not certain on the actual results each team had) is so much lower than what the median should be. I know data is data but seeing how the odd this is all seeming I’m thinking about just throwing out 2009 all together (and will therefore have to throw out the 2009 counting stats too).
Also, has anyone given any thoughts to the effect of the Astros moving to the AL is having on historical data in mono leagues? Comparing the 2013 data my regression lines are not as steep but I’m not sure how much that has to do with the Astros based on one year of data. If there is an effect I’m not exactly sure how to quantify and adjust for it.
KG, you ask a number of really good questions. I’ve always played in standard mixed leagues, so I’ve never run into these issues myself before. But these questions have me giving long looks at the other ranking approaches (PVM and z Score), because they’re not so dependent upon league history. They are inherently “forward looking”, whereas SGP is looking at the past and assuming history will repeat itself.
I hope to eventually write up how to do all three approaches. But I can’t say when I’ll have something like that completed.
I have been thinking about if it makes sense to include league history from 5-10 years ago in SGP calculations because the offensive environment has changed so much. I don’t have any science to back me up, but I am thinking it would be best to eliminate anything prior to 2009 from your calculations. I think it will just muddy the water too much and possibly give you inaccurate results.
Unfortunately when i was working through the pitching data my workaround solution went out the window. When I go and pull player stats from previous years, our site (CBS) didn’t lock/archive what players were actually present. I noticed this while going through last year’s pitcher data and saw Fister show up despite being in the AL last year. I was also noticing that my top 90 pitchers also included several middle relievers who were not rostered during the season which was also throwing off the data.
Since I don’t have reliable historical data (I’m going to make a better attempt this season to keep track of the rate stats), I’m going to have to move on from SGP even though my gut tells me that for established leagues it might be the better way to go. I’m not convinced on PVM on my limited study of it so far, it seems like you need to do too much adjusting by guesswork to balance the individual stats.
Apologies if this was covered somewhere and I missed it…seems like a bit of an obvious question. I’m in a 20 team H2H re-draft league and I can’t seem to find the magic place where it shows past stat totals. Would the SGP for a 12 team league be similar, or do I have to somehow obtain that information (which I’m having trouble finding.)
Sorry if that’s a dumb question, never really got into the nitty gritty world of spreadsheets before and I’m not really skilled with excel. Thanks for this guide, it’s really helped a huge amount.
I think the fact that there are 20 teams will affect the SGPs. Being a H2H league also complicates things because it is a legitimate strategy to punt one or more categories in H2H leagues. But I don’t suspect it will affect things too much. The players you establish as “replacement level” will be the biggest difference. What site is your league run from?
Yahoo. Some guys are using z-scores instead and I’m not sure if that’s a preferable method for H2H. I think I’m going to try running with this and see how it works out and also since it’s easier to understand. Would you be able to take an educated guess at the SGP for K/BB?
Thanks.
AT, I can’t give an educated guess. But if you have your historic league standings/results available to you in Yahoo, you can perform a calculation yourself using the tool here. You could just fill it out for the one category you need.
And while I can’t give the SGP calculation, I do discuss an example of how you would calculate it above in this comment.
Tanner,
Just found your site recently and have been enjoying what I’ve seen so far! Nice writeup on SGP, I’m personally a bigger fan of using z-scores (and using historical stats for std devs), but the concepts seem essentially the same.
Question time: I’ve been wrestling with an issue lately that I’ve been personally referring to as the “Hanley Ramirez problem” – certain players, especially elite ones with injury histories, tend to be projected for ~550 PA or less while still managing to be well above replacement level. But are these various methods correctly valuing these players? As you point out in another of your articles, winning teams maximize their opportunities to get more PAs. If Hanley manages to put up 550 PA of elite production, that still leaves you ~100 PA of some other bum rep lvl SS to accumulate more counting stats. Meanwhile Elvis Andrus is projected (Steamer 2014) to put up almost as much value as Hanley, but over a full 650+ PA, so there’s no bonus playing time value to be had.
So, have you come across any methodologies that account for this in some way? Certainly we wouldn’t want to go in the direction of Oliver and try to just normalize every player to the same # of PA’s, but maybe some amount of replacement level performance should be added to a player’s statline, weighted based on something like (650-PA)/650? (Maybe 650 PA would not be the number to go with, but something like avg. PA of above-replacement players at each position)
Hi Ryan, I’ve thought about adding this to my process to see how much it will affect things. I envision it would work similar to how the “Replacement Level” lookup works right now. I think you would have to create some kind of a table that calculates the stat line of the replacement level player ON A PER PLATE APPEARANCE BASIS.
Hanley’s calculation for runs would be:
Hanley’s own baseline calculation for Runs + (650 – 550) * Per PA Runs from the table
Where 650 is the “standard cieling” you adjust everyone to and 550 is Hanley’s actual plate appearances. The difficult part is that i don’t think you can give credit for the full 100 games Hanley misses. Some of those he might not be active, but not on the DL. Some will be normal days of rest, etc. You can’t predict some of that accurately. So maybe multiply the gap by 80% or some other measure.
Great stuff here! Thank you. How would the step by step calculations change for calculating a SGP formula/value for OBP instead of AVG? More variables than just hits and at bats.
I just posted an example OBP calculation here: https://www.smartfantasybaseball.com/2014/02/calculating-standings-gain-points-for-obp/
“I know that it takes about 200 SB to win the category. So I draft players to reach 200 SB. Not 12 SB SGPs”
I would like to know how to compare the SGP of the players you’ve drafted with the SGPs needed to win the league. I feel this would let me know when I’ve over-drafted a stat category and where my needs are to make trades.
For instance, in my fantasy hockey league I calculated the SGPs of the offensive categories for the season thus far.
G P HIT BLK +/-
4.0 11.0 68.7 8.3 5.3
If I total my teams SGPs up I get 65.3 53.6 16.4 59.3 21.4 in those same categories, respectfully. I know I need 49 126 223 121 14 in each to finish just ahead of the 2nd place team. Basically, I’ve got a feeling that my team has overkill in one stat (Hits) while lagging in another (blocks). How can I verify my hypothesis with SGP math? How can I used SGP mid draft to stop drafting a stat I have accumulated enough of and focus on category holes on my team? MUCH THANKS! Feel free to email me.
Hi Sean, for SGP to work well you must have information about the statistics it takes to win a given category. I don’t play fantasy hockey, but let’s just say you know that over the last 5 seasons in your league it has taken an average of 500 hits to win the category. If your team is projected to exceed 500 hits, then you are overkill in the category. There really is no need to overcomplicate things with SGP math.
Your sentence “If I total my teams SGPs up I get…” is worrisome to me because this is exactly what I suggest not to do. It’s much safer to simply know the statistics necessary to finish first in a category and see if your projected stats meet those requirements. When you start evaluating on the basis of SGPs there is a greater room for error and noise in the results.
Maybe I’m just not excel-savvy enough to figure this out, but how could I change things around here to fit the scoring system in my h2h points league? Any help would be great thanks!
Hi Seth. Points leagues do not need to use a system like SGP to rank players. It’s much simpler for a points league. You simply need a set of projections and then multiply those projections by the scoring settings for your league.
For example, I’m in a points league where doubles are 3 points, HR are 9, SB are 3, H are 5, 3B are 5, BB are 3, and AB are -1.
So if a player is projected for 40 2B, 30 HR, 10 SB, 200 H, 5 3B, 80 BB, and 600 ABs, their projected points would be 40*3+30*9+10*3+200*5+5*5+80*3+600*-1 = 1,085 points.
There’s no need to determine SGPs or z Scores or anything like that. You might consider an adjustment for replacement level players though. So if my example player above is an OF and the replacement level OF is projected for 400 points, then I would subtract 400 from every outfielder. The player mentioned above would then have 685 points in my ranking system.
Thanks for the response! Do I just need to make a separate sheet, and do the formula, for example HR * scoring?
Also, how would I figure out a replacement level player? Sorry if these are simple questions, just now getting into the depths of all I can do with fantasy statistics!
I do prefer to do my rankings on a separate tab from the projections, but you don’t have to. I do it on a different tab because it makes it easier to download a new set of projections and drop them into the file without having to redo all the formulas again. But it does take a lot longer to set up initially.
Replacement level is discussed in Part 6, if you haven’t read that yet. But basically you need to know your league size and about how many players will be drafted at each position. If you think 24 SS will be drafted in your league, you can use that 24th SS as replacement level.
Oh duh, that makes perfect sense for replacement level players. Thanks! Love the excel layout!
What would the formula be for k/9 if you calculated the average k/9 was 8.0 for your pitcher pool?
Tanner,
Love the site and your demonstration of SGP. I have a question regarding the example you present in the article. When you mention 14 batter positions, are you counting bench spots? Or just offense position spots?
Thanks again for your work!
Mike
Hi Mike, thanks for the kind words. Are you referring to the calculation of BA SGP? For this calculation, I think it is important to only use the number of starting batter positions you have. If you start 14 hitters, then 14 hitters need to be included in the calculation. The reason for this is that a single player can have a larger effect on smaller starting lineups. The same hitter will have a smaller effect on a large starting lineup.
Awesome. Thanks!!
When calculating the SPG for Batting Average you say “In the Steamer projections, the top 168 major leaguers..” Who are these “top” players? The players with the most ABs? Great site, keep up the good work.
Hi Drew,
This is something I struggled with at first until I figured it out (at least for hitters). Note that I’m using z scores instead of SGPs (I do not have enough historical data for my league setup to do SGPs) I think the method should work just as well.
1) Bring up your entire projection list for hitters and run the calculations for the counting stats (R, RBI, HR, SB) just the same as Tanner has listed above for all of the hitters you have projected.
2) When it’s time to do batting average (or OBP or whatever else you might use), just take the first 168 players on that list, it doesn’t matter what order they are in.
3) Calculate your average ABs and Hits based on those first 168 and apply the calculation to your entire set of players.
4) Calculate your total SGPs for each player.
5) Once you have done that, sort your project list by your SGP totals. This should re-sort the list based on your original averages and give you a new set of 168 to work with.
6) If you setup your formulas so that they update automatically you’ll just need to re-sort your list a few more times until the list stops changing and you should have your 168 (or however many you need with your league setup) hitters. If you’re in a 2 catcher league you may need to add a catcher or two at the bottom of your list.
I tried to do the same thing for pitchers but it hasn’t come out very well, it keeps trying to put a lot of middle relievers in my pitcher set that have a rare chance of getting drafted. I’m trying to find a method that works there but I haven’t been happy with my results so far.
KG, just in case you missed it, there’s a small bullet point at the end of the article about how I approximate who the top 108 pitchers are.
“To calculate a baseline for the rate statistics, I perform a rough exercise to approximate the 108 pitchers most likely to be rostered. I include the 108 pitchers with the highest strikeout numbers and with a projected ERA below 4.20.”
It is an arbitrary starting point, but you could just use this as a starting point and then resort your 108 pitchers and update the calculations for that. Once you have something like that in place it should not allow the relievers ERA and WHIP to weight high enough to get significant SGPs.
I did see that and did something similar when I ranked. I wasn’t particularly happy with it as it’s more subjective but i couldn’t find a formulaic way that I was happy with. I discovered part of the problem was that my spreadsheet was not accounting for at least the minimum amount of innings each team needed to have (our league has a 1000 inning minimum, I’m assuming most leagues have something similar). In my 10 team league that should mean the Top 90 would need to have at least 10,000 innings pitched but when I ran my iterations I only ended up with about 8,300 innings. I’m ok with Excel but coming up with a formula that checks and corrects for this is a little beyond my abilities.
Hey Tanner,
Is it better to try and rank the 108 pitchers likely to be drafted to determine IP, H, BB to use for WHIP and ERA calculation vs using last years league data?
Also to determine which 108 pitchers are likely to be drafted, could you perhaps use team’s depth charts to assist? Would take a bit longer and would need to be done closer to opening day but could result in better results?
Hi Zach,
Indeed, you may get a slightly more accurate answer by running that test closer to the season. But I don’t think the calculation being performed will change much even if we’re slightly wrong about who the 108 are.
The guess about who the 108 are is only used to determine what the baseline ERA and WHIP are. We then plug that baseline ERA and WHIP into the calculations as the “average player’s ERA and WHIP”.
If we wait and find that we had 10 or even 20 of the projected starters wrong, I don’t think that will change that ERA and WHIP of the top 108 much. It might be interesting to see though.
Tanner
Drew, great question. I just chose the 168 hitters with the most projected ABs. But you made me second guess myself. And upon further review, that’s probably not the best means to identify the top 168 hitters.
The method KG describes is probably the best way to identify the top 168. But I also thought it would be helpful to quantify the difference between the two methods.
Above I mention the formula for BA is “=(([@H]+1768)/([@AB]+6617)-0.267)/0.0024”, where 1,768 represents the average number of hits for a team, and where 6,617 represents the number of at bats the average team hits.
That is based upon the average hitter having 509 ABs and 136 H (for a .267 average).
If I look at the top 168 players after I’ve ranked them (and not just the 168 with the most ABs), the average player is projected for 495 ABs (instead of 509).
A .267 BA on 495 ABs would assume 132.2 H (.267 * 495).
That means the average team would have 1,851 H (14 * 132.2) and 6,930 AB (14 * 495). Adjusting that to the 13 players necessary to calculate one player’s impact is 1,719 H (13 * 132.2) and 6,435 AB (13 * 495)..
Running Trout’s 2013 Steamer projection (184 H, 619 AB) through yields the following:
(184 + 1,719)/(619 + 6,435) = 1,903 / 7,054 = .26977 New Team BA.
.26977 – .267 = .00277
.00277 / .0024 = 1.154
So Trout’s SGP on the top 168 players is 1.154. When I ran it on the 168 with the most ABs, it came out to 1.151. So the difference is negligible. But in a perfect world, you should do an analysis similar to what KG suggests.
Would you adjust the SPG formulas posted above if the league is a 10 person league rather than a 12 person league? I’d imagine it would shift the values some…just not sure if it’s significant enough to need to recalculate. Thanks!
There’s only 9 hitters per team in my 12 teamer. Since I don’t have access to past years’ data, would you expect using your/or other public SGP values to be in the realm of correctness?
I think using the SGP method is still sound. But you need to make an important adjustment in the calculations. You need to adjust replacement level for your specific league.
For example, if you’re in a 10-team league instead of 12-team, you won’t use the 24th catcher as replacement level (assuming a 2 catcher league). It might instead be the 20th catcher.
Or if it’s a 12-team league with 9 hitters, you might use the 12th catcher.
You can use the rough SGP calculations, but you HAVE to adjust replacement level for your own league’s roster sizes.
Once you get some final standings for the league, then you could refine the calculations by calculating the SGP factors.
Tanner, I am in a 10 team, mixed, standard 5×5 league. How can I change the formulas in the SFBB-Rankings-Part-4.xlsx for use with my team in this 10-team league? Thanks. I appreciate how you freely share your information. Love this site. Unfortunately for you, I won’t be sharing this site with my league-mates, but perhaps others who play in different leagues.
Hi Matt. Unfortunately, I don’t have an established history for 10-team leagues to draw from. If you have an established league history where you can access prior season standings, you can calculate these things yourself using the “What It Takes To Win Your League” tool.
But even if you don’t have past standings to draw from, I think you will still get meaningful results from using the same formulas I have listed on the site here.
As I mentioned right above here, the very important adjustment you must make is in determining replacement level for the 10-team league. Use your actual roster composition and the fact that you’re a 10-team league to figure out who the replacement level C, 1B, 2B, etc. are in your league.
Hey my league is a 10-team mixed league but only in our second year. Added new GMs as two didn’t even pay attention to their teams last year. So don’t trust the differences in points. You know a place to find 10-team league SPG numbers?
Ignore my question just saw your reply to March 5 post.
Thx
I’m just wondering if I should use different formulas for Starters and Relievers. I’m in a 10 team league with 5 starters and 3 relievers per team. Our categories are W, L, HR against, ERA, K/9, BB/9, H/9, SV. As you can see there are many ratio stats there, so relievers have more value. After doing this exercise however, the discrepancy is too large (all relievers are worth more than any starter).
So let’s assume all my numbers are without error (doubtful), I still wouldn’t pick Kimbrel ahead of Kershaw, no one would, but if I separated out the RP and SP, I could wait til people start picking relievers and use my RP list a that point.
I could use the IP and ER averages for the top 50 starters, and do the same for the top 30 relievers and make separate ranks. Maybe I’m way off track.
Thoughts?
Maybe not my place, but my way of getting around this issue was simply converting ratio stats into counting stats. My excel formula looks like this: =([@ER]*9-([@IP]*AVERAGE($Q$2:$Q$264)))*-1 where Q is ERA. This works for any stat, take the numerator and multiply by the denominator*the league average for that ratio stat. I went with z-scores over SGP in the end (lack of league history plus I think SGP works better for roto leagues, I only play 20 team H2H) so I am not sure how you would calculate SGP from that.
*subtract the denominator, not multiply, sorry.
You will want to treat those categories like Tanner has treated the other ratio categories. “Does the fact that Trout will hit .297 over nearly 200 more at bats make him more valuable? Or does Tulowitzki’s .300 average make him the better “batting average contributor”?” Think 200+ IP of Kershaws’ K/9 vs 60 IP of a Kimbrel.
Hi Jimmy. If your categories really are W, L, HR against, ERA, K/9, BB/9, H/9, and SV, then I think it makes sense for relievers to have more value than starters. A reliever will have fewer losses, fewer HR against, a lower ERA, better ratio stats, and more saves. The only benefit to having starters is the W category.
I do not think it’s necessary to treat SP and RP as different groups. But you should calculate replacement level separately for the two groups. The calculations will all be the same, but starters will be compared to replacement level starters and relievers compared to replacement level relievers.
If you follow the formulas for weighting the stats, you’ll be fine.
Hey thanks AT and Drew,
AT – Where do you find z-scores? I must have missed something.
Drew – I agree, I’m just thinking from a strategy point of view; with our cats, my numbers say RPs are worth the most, but strategically it doesn’t make sense for me to pick RPs in the 3rd round for e.g. So I’m just looking for relative value between SPs and RPs, I understand the contribution aspect, but I will just use my RP list when guys start drafting RPs.
Z-scores are different from SGP and simpler to integrate. You just standardize all the stat columns your league uses and add them together. For example, my z-scores for K/BB: =STANDARDIZE([@XKBB],AVERAGE($T$2:$T$180),STDEV($T$2:$T$180)) Where T is XKBB, which is K/BB converted to a counting stat. Then you just mash them together. My rankings passed the sniff test, so I’m happy with it. It’s just an alternate to SGP.
My league is switching over from AVG to OBP. Any advice on adjusting ranking calculations for OBP without inflating its overall weight?
PEDex, here’s a link to a discussion of how to calculate SGP for OBP.
Tanner, being a neophyte at ;Excel, I do not know how to do this one thing other than manual. I would like to grab the PlayerID, LN, FN, POS, and TTLSGP columns from both the Hitter Ranks and Pitcher Ranks tables and merge them into one worksheet and table so I can compare the pitcher and hitter Totals at a glance w/o having to toggle back and forth between sheets. How do I do this? I will have enough to do on draft day (two draft day software pkgs. [I might buy a 3rd b4 DD], and at least three spreadsheets besides your SGP sheets). So, I don’t want to be toggling any more than necessary. BTW, just bought the entire 10 chapters so I could read up on the impact of keepers; I am in a keeper league.
Thanks
I’m seeing this article almost two years later, but…
When calculating the SGP value of AVG, for example, what’s the advantage of using the Razzball average AVG (or even the average AVG from one’s own fantasy league) as opposed to using the projected average of those top 168 hitters per the projections? Given the yearly changes in the MLB run-scoring environment, wouldn’t using the projected averages of those players provide a better baseline?
I’m assuming, of course, that projections consider those trends, which they do, b/c they consider the trends in each individual player’s production. If there’s a league-wide decline in AVG, that’s the culmination of individuals’ AVGs declining.
But previous year’s data, taken statically, doesn’t account for that.
Bert, yes. I’m completely in agreement with you. Instead of using the .267 BA, 3.59 ERA, and 1.23 WHIP I pulled from Razzball at the time of this article, I would rather determine what the projected BA is of the top 168 hitters and what the ERA and WHIP are of the top 108 pitchers, and then use that as my baseline.
The other thing this does is it will conform more precisely to your league size. I always calculate things for a 12-team league with 9 pitchers. If your league has more or less teams or more/less roster spots, the ERA/WHIP of those players will surely differ slightly as you are deeper/shallower in the player pool.
Thanks, Tanner. This is all really good stuff, and it’s already been super helpful as I create dollar values and rankings for my leagues.
Anytime. Let me know if you have any more questions.
Hi Tanner, This is my first time trying to do my own dollar rankings, and I’ve found your guide to be very helpful and straight forward. I am in a 22 team mixed league though. We start 9 hitters and 9 pitchers, (6 SP and 3 RP). I’m just wondering how I can calculate the AB’s, Inn’s etc. for the ratio categories. Based on the above answer, could I just figure out the avg # of AB’s for the top 198 Hitters (9×22), 132 SP’s, and 66 RP’s?
Hi, Brett. I’m glad you’re finding the site helpful. I don’t normally suggest differentiating between SP and RP for replacement level but I think you are correct to try that in your situation. Normally we would not see that kind of depth in the relief pitcher pool, but by requiring 66 of them to be rostered, you’re in a unique situation.
I think your approach of figuring out the average # of ABs and IP for the top 198 hitters, 132 SPs, and 66 RPs is correct. Keep in mind that it’s not just the “top 198 hitters”. Ideally it would be the “top 198 hitters already adjusted for replacement level”. If you just take the top 198 hitters, I’m guessing you won’t end up with 22 catchers.
The issue with this is that it is a bit of a circular calculation. How can we figure out replacement level if we don’t know how many ABs will be in the top 198 hitters? You might figure out who you think the top 198 are, then figure out the ABs for those players, then adjust your BA SGP calculation and find out that now your top 198 are different. Fortunately, I’ve found that it will not change the SGP calculation significantly.
I don’t mean to confuse you by throwing in that last discussion. You could start with the straight up top 198 with no regards to position, figure out the average ABs, figure out your SGP formula, then figure out replacement level, and then redetermine the top 198 and then check your average AB calculation again. I don’t think you’ll find this causes a big change in anything.
I worked through it this way, and find AVG to very under represented. The top producers in R, HR, RBI, and SB’s all earned 8-10 SGP’s, whereas the top in AVG only earned about 2-4 SGP. The numbers I used were 4500 AB’s, a .262 avg,and 1205 total hits. Any suggestions on what I can do to fix this? Thanks for your help…
Feel free to e-mail me your spreadsheet and I can look things over. But I don’t think there’s necessarily an issue just because the top AVG earners have a lower SGP than the counting stats. Keep in mind that AVG is fundamentally different than the counting stats of R, HR, RBI, SB.
In those counting stats a player that has 0 HR gets 0 SGP. He cannot have negative SGP. But for AVG, a player with a below average BA actually does get a negative SGP calculation. So a hitter with a +4 SGP needs to get compared to the negative SGPs of the worst BA for your true picture of the spread. It might be that the players with the worst BA SGP have a -5. So comparing -5 to a +4 you’re still getting a spread of 8-10 SGPs between the worst and best players.
Having trouble with calculating K/9 and BB/9. I have the Denominator for K/9=.09 and BB/9= -.09. 14 team league 10 pitchers (5 sp 5 rp) calculate the top 140 pitchers projected K/9 using ERA under 4.2 and top K/9 that would be rostered. Obviously average out my leagues average for both stats, would the formula look something like (TOP140K’s with 9 pitchers + proj K’s)/9/(Top140IP + Proj IP)-LeagueaverageK/9/.09 for K’s ? and then (TOP140BB/9 with 9 pitchers + Proj BB’s)/9/(Top140IP + Proj IP)-LeagueaverageBB/9/-.09 ?? Thanks, let me know if any one else can help out with calculating these two.
Hi, Anthony. Please figure out who you think the top 140 pitchers are in your league, but I just ran a really quick calculation for an example:
Top 140 pitchers:
22,115 IP
19,037 Ks
7.75 K/9 (19,037/22,115 * 9)
Dividing those grand totals to get a per pitcher average:
158 IP
136 Ks
9 of those pitchers would be:
1,422 IP (9*158)
1,224 Ks (9*136)
So I think the calculation would be:
([(1,224 + PlayerXStrikeOuts)/(1,422 + PlayerXInningsPitched)]*9 – 7.75)/0.09
My determination of the top 140 pitchers was really weak (I think RPs are underrepresented in my top 140 if you need 90 of them for your league), so please determine that on your own. That might make your IP and Ks quite different, but just swap them out in my example formula once you have your own. My daughter just woke up from nap though! That’s the best I have for now.
If I run Kershaw through that formula I get SGP of 3.17 for him. And this is a rate stat, so that will be compared to other pitchers who will end up with a negative SGP for this category.
This worked great Tanner thanks! Ended up with Kershaw having a K/9 SGP at 2.15 and bb/9 SGP at 1.24. Wasn’t too worried about these since its so miniscule in my league, but wanted it nonetheless, thanks for all your help!
Tanner, do you notice that your top end players (hitters mostly) don’t have the nearly the same high end values that you see on other value sites? For example, in my 14 team 2 catcher 5 OF league $260 cap 67/33 split, I have only 3 hitters above $30. When I know Trout, Miggy, etc. have values over $40. I feel like when calculating using historic SG it creates a ton of players in the $10-20 range and not as many in the higher or lower ranges.
I’ve had success the past two years just with basic knowledge that I’ll have to spend more early, well above my projected values, but can’t seem to get it balanced like I’d prefer. I use steamer for my projections.
Thanks
Hi, Dan. I just ran a test on the league settings you described and I do get Trout over $40 and then Cabrera and Stanton right around $38, then 6 more players also over $30.
Do you have a lot of bench players in the league that you’re trying to reflect in the values too? They could be draining some of the money from the top players.
Hi Tanner,
Working on my preseason. I’m in a 5×5 AL only roto league with 14 hitters and 9 pitchers. We have a bunch of keepers, but I’m trying to evaluate who is worth keeping based on my preseason work. So far I’ve done well, but now I’m on figuring ERA and WHIP. Based on my leagues history the Razzball averages are too low. To figure average ERA and WHIP do I simply take the average of our 12 teams over our history and use that as the basis for our average ERA and WHIP to create my own formulas?
Did some math, over the last 4 years, our leagues average ERA is 3.97 and our average WHIP is 1.29. Are those the numbers I should use in your formulas for calculating TTLSGP or should I use different numbers?
Hi Chris,
You could use historical averages, but I think I would prefer using the projected stats for the coming season. I looked at my projections for the top 108 AL-only pitchers and it looks like they will pitch 13,850 innings, giving up 5,750 earned runs for an ERA of 3.74 and a WHIP of 1.2574.
I think this is best because we are trying to figure out a pitcher’s impact on our ERA for this season, and our best guess of what those numbers will be are included in the projection
Hi Tanner,
Thanks for answering my question! One more, without using TTLSGP how did you determine the top 108 pitchers? Did you use the same formula you use in your book, the top 108 pitchers based on strikeouts for pitchers under 4.20 ERA?
Hi Chris, this is a “circular calculation”. I take a guess at what the average ERA and WHIP will be and then figure out all of my SGP using that (including TTLSGP). Then once I have that I can “fine tune” the ERA and WHIP SGPs for the top 108.
After you change your ERA and WHIP formulas, the top 108 will probably change slightly. We could go into this continual loop. “Edit the ERA”, “redetermine the top 108”, “Edit the ERA”, etc.
Hi Tanner
Another question. I used steamer projections for 2015 and ran into the same problem as dan. Only trout and Bautista are ranked above $30. I think I may need to run through the projections more carefully from steamer to be sure I have the correct info. I followed each step in your book to the letter. The only exception is I calculated slope numbers from my leagues historical data, used the numbers you gave me yesterday for whip and era and figured my own numbers for batting average based on the average of our leagues history. I could change the average to match the numbers from the top 168 in the projections that is my next step.
I also did a 70-30 split and noticed the top pitchers are valued lower than in my league but the middle level pitchers are valued about right. most likely my league just over values the top 6-10 pitchers. Do you see that often?
Hi Chris, if you think your dollar values look odd, the first thing I would do is to double check your replacement level information. I found myself making a lot of mistakes with this part and found that it takes a long time to do, so I created a video to demonstrate the approach I’m using now. You can see it here.
If you see that your pitchers in your rankings are undervalued (in comparison to what you actually see on draft day), you could adjust your split downward. Try 65-35 and see if that aligns pitcher values better with your league.
First of all just want to say thanks for all the great work. I think I have run into a little problem though. I’m stuck at part 6 because after calculating SGP my rankings are crazy. A lot of closers are ranked at the top in pitching categories. I have 3 pitchers ranked higher than Kershaw. I have Altuve, Jacoby Ellsbury, Brett Gardner, Starling Marte, Billy Hamilton, and Dee Gordon ranked in the top 10 hitters. While I think s little error is normal this just seems crazy. Here is my league settings:
H2H Points League 12 Teams
1 C, 1 1B, 1 2B, 1 3B, 1 SS, 1 MI, 1 CI, 4 OF, 1 DH, 7 P and 6 bench spots
Scoring:
Batting- singles 3, doubles 5, triples 8, home runs 10, walks 2, runs scored 2, runs batted in 2, stolen base 5, hit by pitch 2, caught stealing -2.
Pitching- innings pitched 2.25, earned runs -2, wins 4, saves 10, strikeouts 2, hits allowed -0.6, walks issued -0.6, shutouts 2.5, hit batsmen -0.6, complete games 2.5, no hitters 5.
I Tried to calculate SGP for R, HR, RBI, SB, H, 2B, 3B and W, SV, IP, BB, SO, and then I did era because CBS would not give me our leagues ER.
I don’t know if this is wrong or not but it is producing crazy results like I said earlier.
Should I tailor part 5 to my league and if so, how?
Once again thanks for all the help!
And when I say I have crazy pitcher rankings, I mean that all closers are 1-26 and then I have 5 more pitchers ahead of kershaw, 3 of which are SP.
Hi Matt, it sounds like you’re in a points league. Standings Gain Points should be used only for rotisserie format. I do have a separate set of instructions for points leagues here.
Okay awesome thank you! And is there a way to convert those rankings to $ value form auction drafts? Will purchasing the book and using parts 7-10 work?
The “Using Standings Gain Points” book will also only help you calculate dollar values for rotisserie leagues. I’m working on a dollar value book for points leagues. Stay tuned on that one!
Tanner,
Is SGP a useful concept for head-to-head leagues? If not, what’s the best approach to converting projections to ranks or dollar values for such a league?
Zach
Hi Zach,
SGP exactly as I write about it does not apply to head-to-head, but with a slight tweak you could use it. Instead of determining SGP on the season ending statistics, you could grab several (or all) weekly standings data and run the SLOPE function on those weekly standings.
I think this is still a little imperfect for H2H because many managers don’t try for a balance strategy in that format. You’re incentive is to win the week, not perform well across the board in all categories. You may want to research the Percentage Valuation Method or z Score approach for something that applies better to H2H.
Thanks,
Tanner
HI,
Thanks very much for this. Can I use this for an 8 team league? I know it is a pretty major difference, but won’t it still yield similar results (who is undervalued, where each ranks relatively, etc.)?
Thanks!
Brendan
Hi Brendan,
I think you’re dead on here. I think you can use these SGP factors, especially if you’re happy with just seeing relative ranks. Might you get a little more accurate / different results if you had a history for an 8-team league, yes. But in all likelihood going from 12 to 8 teams is only going to shrink the gaps in the standings, but it will probably shrink it proportionately. For example, I wouldn’t envision that the home run category gets significantly closer and the stolen base category gets more spread out.
I have a league that fluctuates between 11 and 13 teams in any given year and I use the same league history regardless of number of teams. It’s possible my values are slightly skewed because of this but I don’t get that sense.
Tanner
[…] for player valuation for your own fantasy baseball league, using a model based either on Standing Points Gained above replacement, or Fantasy Points above replacement, depending upon the scoring system of the […]
Tanner:
I play in a 20-team league with 28 man rosters. At a minimum, you must start 23 players, comprised of either 14 hitters, and 9 pitchers OR 13 hitters, and 10 pitchers (the difference is the utility can be a hitter or a pitcher). Historically, teams draft 16 hitters and 12 pitchers.
I am struggling to decide what numbers to use as a basis for my calculaiton of Standing Points Gain for the ratio stats. A couple of options:
Go with average number of players drafted as follows:
20 teams * 16 hitters = 320 hitters
20 teams * 12 pitchers = 240 pitchers
OR
Go with active roster sizes as follows:
20 teams * 13 or 14 hitters = 260 to 280 hitters
20 teams * 9 or 10 pitchers = 180 to 200 pitchers
Any thoughts? Obviously, this impacts how I arrive at the total expected ABs, Hs, IPs, ERs, etc.
Thanks!
Mark
Hi Mark,
I don’t have hard evidence to support this, but I can give you my line of thinking. It is only players in the starting lineup that contribute to team statistics, so I would use the “active roster” option. I would try to estimate how the teams in your league do this in practice. Does it break down that about half the teams start 14 hitters and half start 13? I’m sure it even fluctuates during the season, but give your best estimate.
So maybe it’s 20 teams * 13.5 hitters = 270 hitters
Tanner
Are there any historical category resources for QS and OBP? We just switched this year and I feel like it’s a major inefficiency to exploit in my league, but I have no idea what my targets should be.
Hi mtnaesthetic, I don’t have this currently. I just put out a request on Twitter to see if any followers might be willing to share. Stay tuned…
I’m new to the SGP conversation and am prepared to learn that I’m way off base here. Disclaimer aside…
I am uneasy with the potential for players to be given a negative SGP value in the ratio stat categories. It really shouldn’t be treated differently than the counting stats, should it? A player below league average does not have a negative value in the home run category.
I do understand that player A’s .230 average “drags down” player B’s .300 average, whereas player C’s 1 home run has no effect on the 30 that player D hits. However, the points should be considered at the TEAM level because that’s what we’re after. In this sense, hitting only 1 home run is just as harmful as having a .230 average.
What if I draft 14 players with averages ranging from .230-.250? The model would give me a negative SGP. If I draft 14 players who hit 0 homers, I end up with 1 “point” for that category and the model will reflect that.
My solution would be to change the comparison you’re doing to value one player:
from this:
the average 13 man team + PlayerX
(minus)
the average 14 man team
to this:
the average 13 man team + PlayerX
(minus)
the average 13 man team + Player0
To find Player0:
1 – calculate the projected team BA for the average 13 man team + PlayerX for every player in your universe. Might want to exclude anyone who isn’t projected for 450 AB or more. You’re probably not drafting someone who won’t anyway.
2 – Find the lowest…this is Player0
It’s not different than finding value for the counting stats. You’re effectively assigning the player a numeric value based on what he adds over the worst possible (and practical) outcome in each category.
In the end, if I draft a bunch of .230-.250 players, the calculations should tell me I’m going to gain zero in the AVG category. Same as 0 HR.
But what’s the true impact?
Honestly, NONE, in practical terms. The deltas between players are what matter. And this change shouldn’t affect the order players are ranked in within the category or their relative worth overall. It just puts the ratio stats on the same scale as the other categories.
If there IS a danger, it would be that of perception while drafting. That people might under-prioritize the ratio stats because their scale, while relatively correct between players, is between -W and Y, rather than 0 and Z like the counting stats.
In fact, you could probably get pretty close to the same answer by calculating the difference between the current SGPs and the worst SGP in the player universe for that category. Doesn’t address the player 0 gripe, but should be directionally correct.
Thoughts?
Hi White Sock,
I do want to start by emphasizing one point you make, “What’s the true impact? Honestly, none, in practical terms… This change shouldn’t affect the order the players are ranked in within the category or their relative worth overall.”
I think that’s very well said. It was the thought I had in mind as I started to read your comment, but you said it better than I could have myself.
I do see a lot of merit in the change in calculation method that you propose. Have you tried this? I’d be curious to see what you come up with if you compare the method I wrote about to your proposal. What kind of change in dollar values for players might we see?
If you have not had an opportunity to try this, I will try to keep it on my radar for something to try next preseason.
Thanks for the suggestion.
Tanner
Quick question as this is my first time calculating SGPs: How do you define “top” batters when determining the # of at bats for the “top” 168 batters? Is this by the top 168 batting averages or the “top” fantasy players by earnings (and if it’s the latter, is that determined by the 2015 actuals or 2016 projections?)
Trying to avoid the old saying: Garbage in, Garbage out! (when it comes to modeling)
Same applies to ERA and WHIP too.
Many thanks!
Hi Zack,
I figure this out in a pretty simplistic manner. I just sort the 2016 projections by at bats. For the most part, we end up drafting any player that plays full-time in the top 168, so it’s not that far from who the top 168 actually are.
You could get more involved here and make this a circular calculation. You can run the numbers first using the approach I just mentioned. And then when you’re all done, figure out who the top 168 actually are. Then take the numbers from that 168 and adjust your formulas to these new inputs.
You will probably find that doing that does not have much of an impact on the rankings.You can apply these same principles to the pitching categories. Just sort by IP to get the top 90 and go from there.
Hope that helps.
[…] hundreds of thousands of words about this topic, and most try to quantify it via something called Standings Gain Points, which I only have a loose grasp on. Basically, it tells you how many Rotisserie points your team […]
[…] I calculated a basic 12-team Standings Gain Points (SGP) value for each position. The formula helps to standardize different stats to a similar reference level. […]